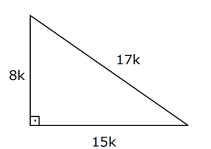
Bu yazımızda 30 60 90 Üçgeni, 45 45 90 Üçgeni, 30 30 1 Üçgeni, 15 75 90 Üçgeni, Üçgende İç Açılar Toplamı, Dış Açılar Toplamı, Roket Kuralı ve çok daha fazlası hakkında bilmen gerekenler ile Üçgende Açılar konusuna ait soruları çözerken işine yarayacağını düşündüğümüz ipuçları yer alıyor Umarız15 75 90 üçgeni 30 60 90 üçgeni 37 53 90 üçgeni 45 45 90 üçgeni 02 Ağu 13, 1933 People also love these ideas Bu şekilde kalıcılığı ve öğrenmeyi sağlıyoruz トップ 75 90 üçgeni özelliği Dik Ucgen Ozellikleri Nelerdir Egitim Haberleri üç kenarı ve üç köşesi bulunan üçgenlerin 4ÜÇGENİ Kenar uzunlukları 8, 15, 17 sayıları ile orantılı olan üçgenler dik üçgenlerdir

15 75 90 Ucgeni Not Bu
15 75 90 özel üçgeni özellikleri
15 75 90 özel üçgeni özellikleri-EB 6 birimdir O halde; Üçgeninin özelliği ile ilgili bilgilerinin paylaşacağı bu yazımızda örnek bir görsel üzerinden anlatımları yapacağız sevgili arkadaşlar Üçgeni Yukarıdaki ABC üçgeninde A açısı 67,5 derece, B açısı 90 derece ve C açısı da 22,5 derecedir




Geometri Formulleri Sezgin Oner Matematik Yayinlari Facebook
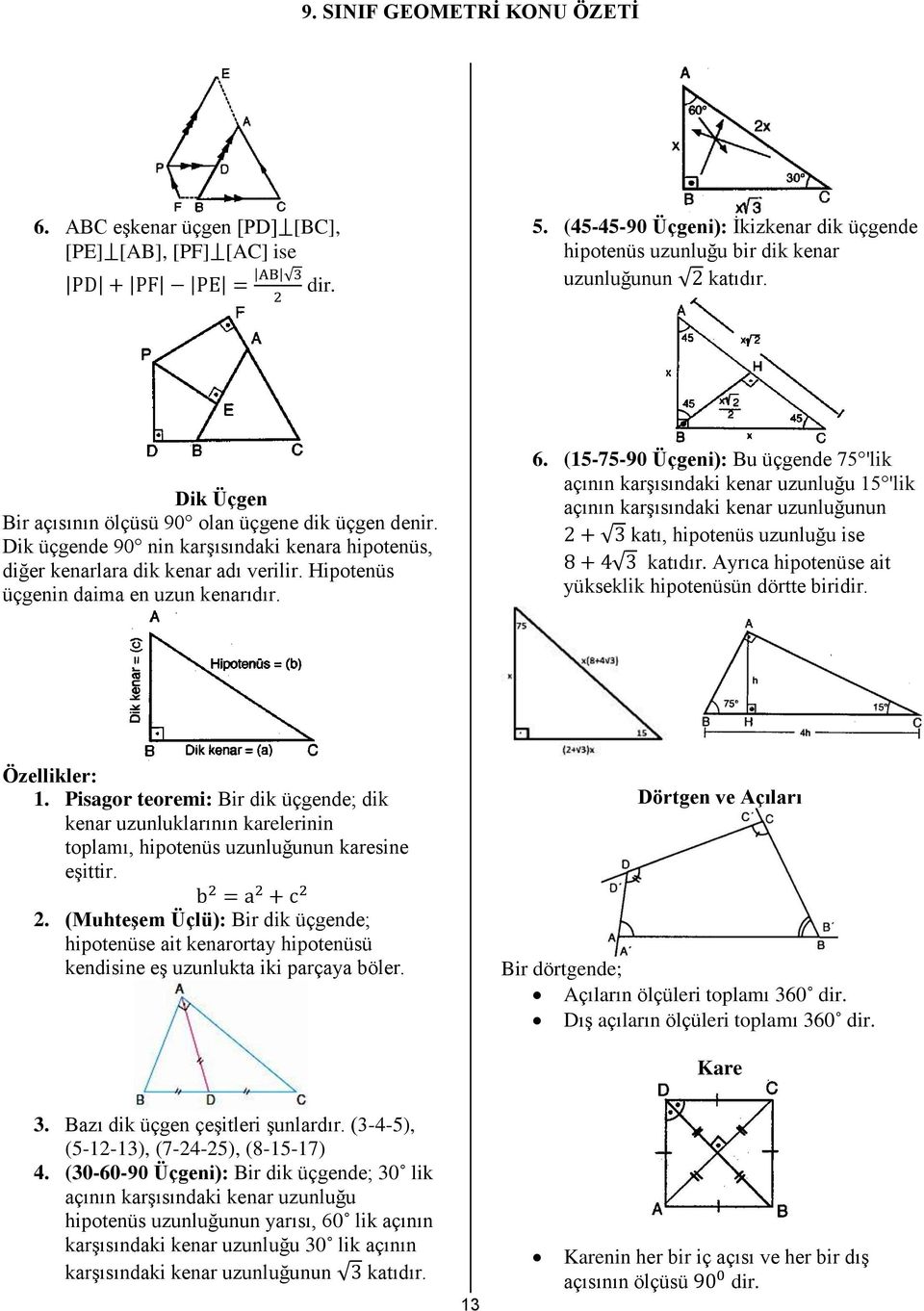
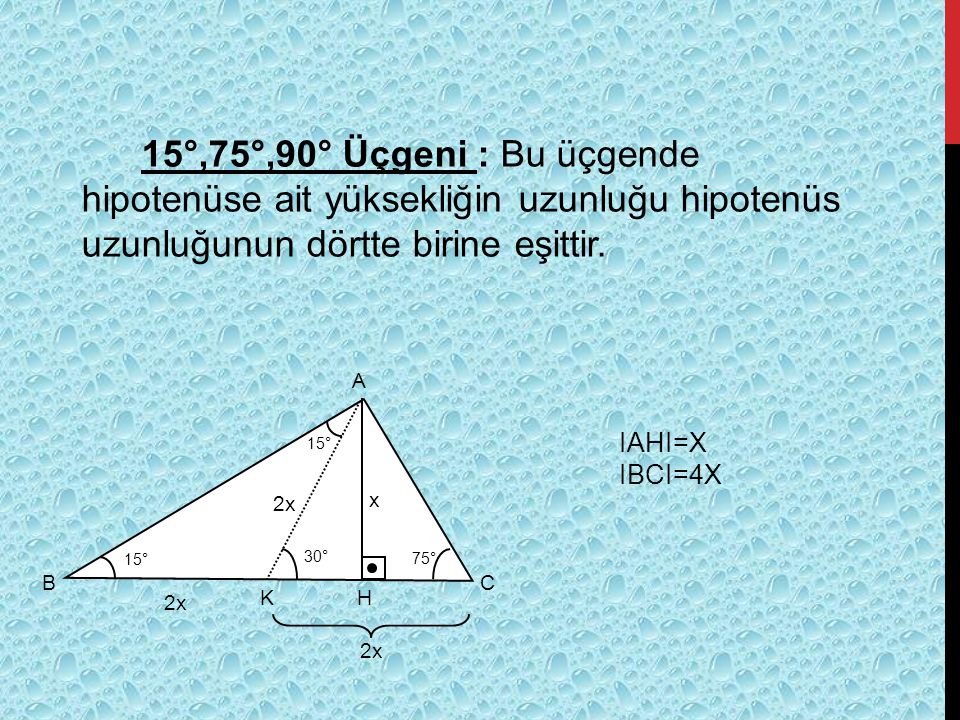
7 (30° 30° 1°) Üçgeni (30° 30° 1°) üçgeninde 30° lik açıların karşılarındaki kenarlara a dersek 1° lik açının karşısındaki kenar a 3 olur 8 (15° 75° 90°) Üçgeni (15° 75° 90°) üçgeninde hipotenüse ait yükseklik AH = h dersek, hipotenüs BC = 4h olur 15 75 90 ÜÇGENİ ÖZELLİKLERİ 15 75 90 üçgeni bir dik üçgendir İç açıları toplamı 180 derecedir Dış açıları toplamı 360 derecedir İki dar açısının toplamı diğerSoru Sor sayfası kullanılarak Özel Üçgenler konusu altında üçgeni ile ilgili sitemize gönderilen ve cevaplanan soruları içermektedir Bu soru tipine ait soruları ve yaptığımız detaylı çözümleri aşağıda inceleyebilirsiniz
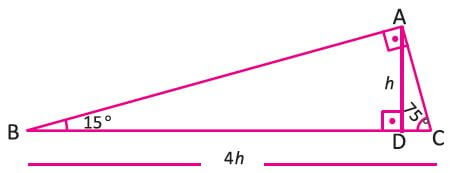
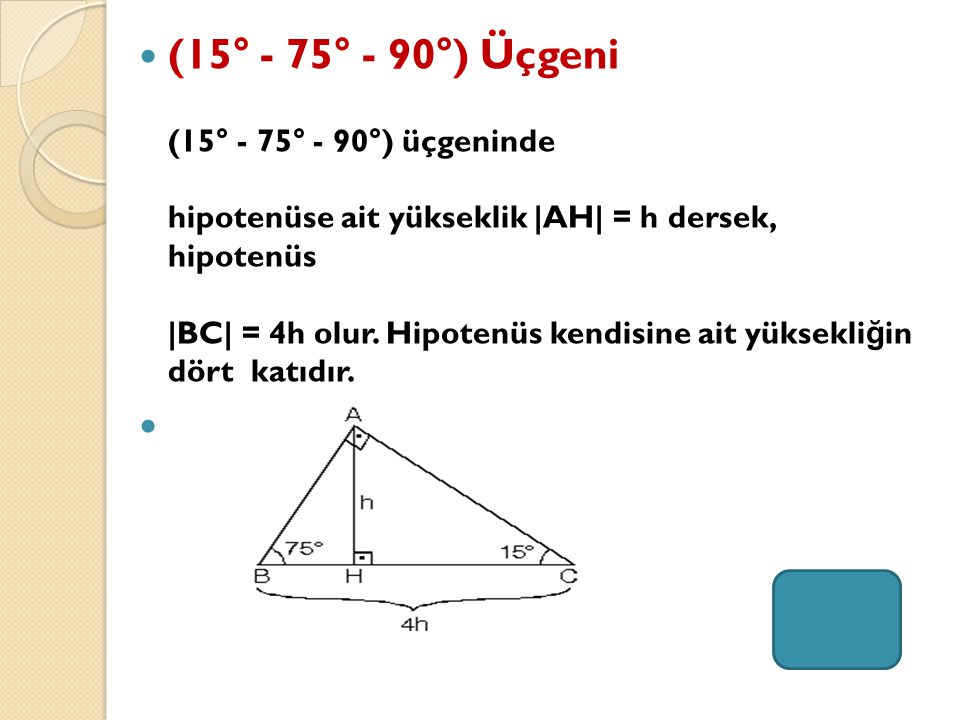
(15° 75° 90°) Üçgeni (15° 75° 90°) üçgeninde hipotenüse ait yükseklik AH = h dersek, hipotenüs BC = 4h olur Hipotenüs kendisine ait yüksekliğin dört katıdır ÖKLİT BAĞINTILARI;üçgeni 22,5 derecenin karşısındaki kenar " a " ise 67,5'un karşısındaki kenar " aakök2 " dir bir de hipotenüs ile ona ait yükseklik arasında bi bağıntı vardır hipotenüse ait yükseklik " h " ise hipotenüs " 2kök2h " dır düzgün sekizgende çok karşımıza çıkar düzgün bir sekizgenin en uzun veyaDik üçgenlerde hipotenüse ait yüksekliğin verildiği durumlarda benzerlikten kaynaklanan öklit
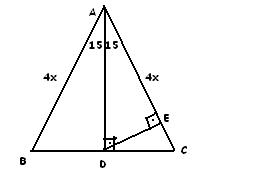
1575 90 Üçgeni Bu üçgende hipotenüsün yüksekliğine x dediğimiz zaman hipotenüsün uzunluğu bu ölçünün 4 katı yanı 4x olmaktadırBulunur ABE üçgeni (15 75 90 ) üçgenidir ABE üçgeninde E nin AB ye en yakın uzaklığı hipotenüse ait yükseklik; özel bir dik üçgendir 90 derecelik açının karşısında hipotenüs bunulunur Bu 90 derecelik açının olduğu yerden hipotenüse indirilecek dik (yani yükseklik) h olursa hipotenüs de 4h olacaktır




Acilar Ve Ucgenler
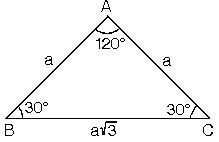



Dik Acili Ucgenin Kenar Ve Aci Ozellikleri Nedir
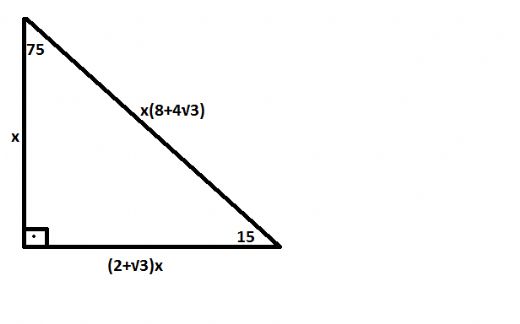
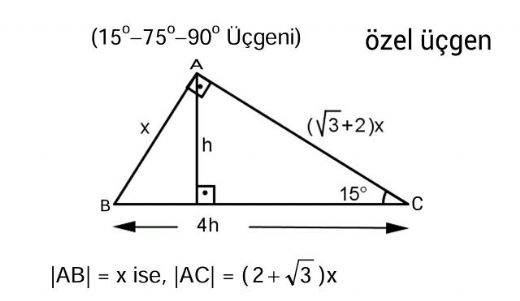
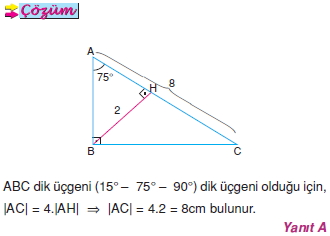
15 75 90 Üçgeni kuralı geometri dersinde özel üçgenler konusu adında yer alır Diğer özel üçgenler kadar yoğun bir şekilde soru öbekleri bulunmasa da çıkabilecek az sayıdaki sorularda ayırt edici problem şeklinde kendisini belli öder15° – 75° – 90° Dik Üçgeni Yukarıda verilenlere göre, AC kaç cm dir?5 (30° 30° 1°) Üçgeni (30° 30° 1°) üçgeninde 30° lik açıların karşılarındaki kenarlara a dersek 1° lik açının karşısındaki kenar aÖ3 olur 6 (15° 75° 90°) Üçgeni (15° 75° 90°) üçgeninde hipotenüse ait yükseklik AH = h dersek, hipotenüs BC = 4h olur



15 75 90 Ucgeni Kenar Bagintisi Ispat



Geometri Webders Net
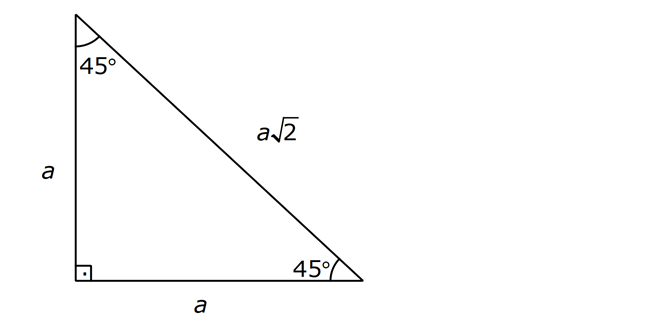
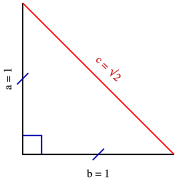
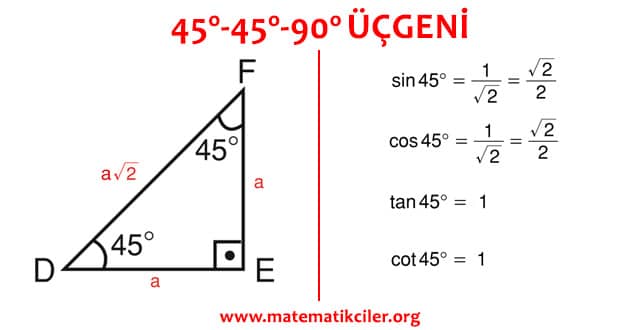
Veya 2 x eşittir 90 iki tarafı da 2'ye bölersek, x'i 45 derece olarak buluruz İkizkenar dik üçgenin daha sıklıkla kullanılan ismi, üçgenidir Bir önceki video da üçgeni için yaptığımız gibi, bu videoda bu sefer üçgeninin kenar oranlarını bulmak istiyorum(15 75 90) Üçgeni (15 75 90) Üçgeni konusunu önce anlatıyoruz hemen ardından etkileşime geçmesini sağlıyoruz Bu şekilde kalıcılığı ve öğrenmeyi sağlıyoruzQuote Orijinalden alıntı brknzbz üçgeninde şu bağıntılar vardır 1 (kök31)k (kök31)k (2kök2)k sırasıyla derecelerin karşılarındaki kenarların aralarındaki bağıntıdır bu 2 15 derecenin hemen yanına doğru bir doğru parçası indirerek ikizkenar üçgen oluşturup (1515 derece şeklinde) küçük bir 0 ve üçgeni oluşturmak




Ucgenler Ozel Ozel Ucgenler Ucgen Cesitleri Ucgenlerin Ozellikleri Pisagor Bagintisi Ile Ilgili Konu Anlatimlar Matematik Dersi Ile Ilgili Konu Anlatimlar Ornekler Cozumlu Sorular




15 75 90 Ucgeni Pow Bylge
Buna göre, Bazı dar açıların trigonometrik değerleri aşağıda verilmiştir Bu değerlerin çok iyi bilinmesi soruları daha hızlı çözmenizi sağlar 30 – 60 – 90 Üçgeni 45 – 45 – 90 Üçgeni 30 – 1 – 30 Üçgeni 15 – 75 – 90 Üçgeni Örnek1 Aşağıdaki ABC dik üçgeninde AB = 5 cm 15 75 90 üçgeni Matematiğin geometri dalının özel formülü olan özel üçgenlerinden birisidir 15 75 90 üçgeni kendine has kuralları olan bir üçgendir ve kuralları değişmez zaten değiştirildiği takdirde açı ve uzunluklarından ötürü özel üçgen olmaktan çıkar Bözel üçgenler (30°60°90° üçgeni) özel üçgenler (15°75°90° üçgeni) öklit teorimi



Ozel Dik Ucgenler Delinetciler Portal



15 75 90 Ucgeni Ozelliklerinin Ispati Youtube
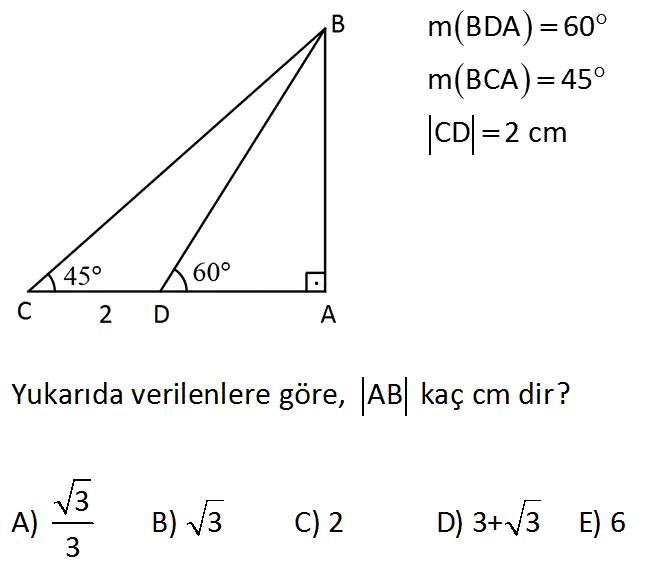
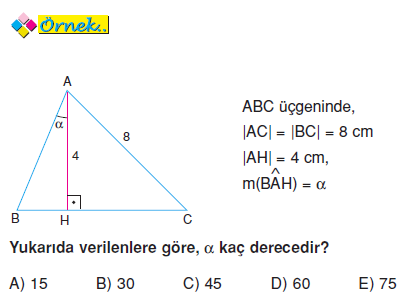
Geometri dersinde bilmemiz gereken bazı özel üçgenler bulunmaktadır Bu özel üçgenler arasında 15 75 90 üçgeni de bulunmaktadır 15 75 90 üçgeni sorularda ve sınavlarda sıkça karşımıza çıkan bir üçgendirA)8 B)6 C)5 D)4 E)3 30° – 30° – 1° Üçgeni 1° nin karşısındaki kenar, 30° nin karşısındaki kenarın katıdır Yukarıda verilenlere göre, x kaç cm dir?12 A B C E 75 15 H 15 x EH = x uzunluğudur Buradan AB = 4 EH olduğundan, 12 = 4 x x = 3 br bulunur Cevap A'dır (vii)(30 30 1 ) ÜÇGENİ A B C 30 30 1




Dik Ucgen 15 45 45 90 Ucgeni Evde Egitim Ders Calisma Ipuclari Matematik




15 45 1 Ozel Ucgeni Var Mi Varsa Kurali Nedir Eodev Com
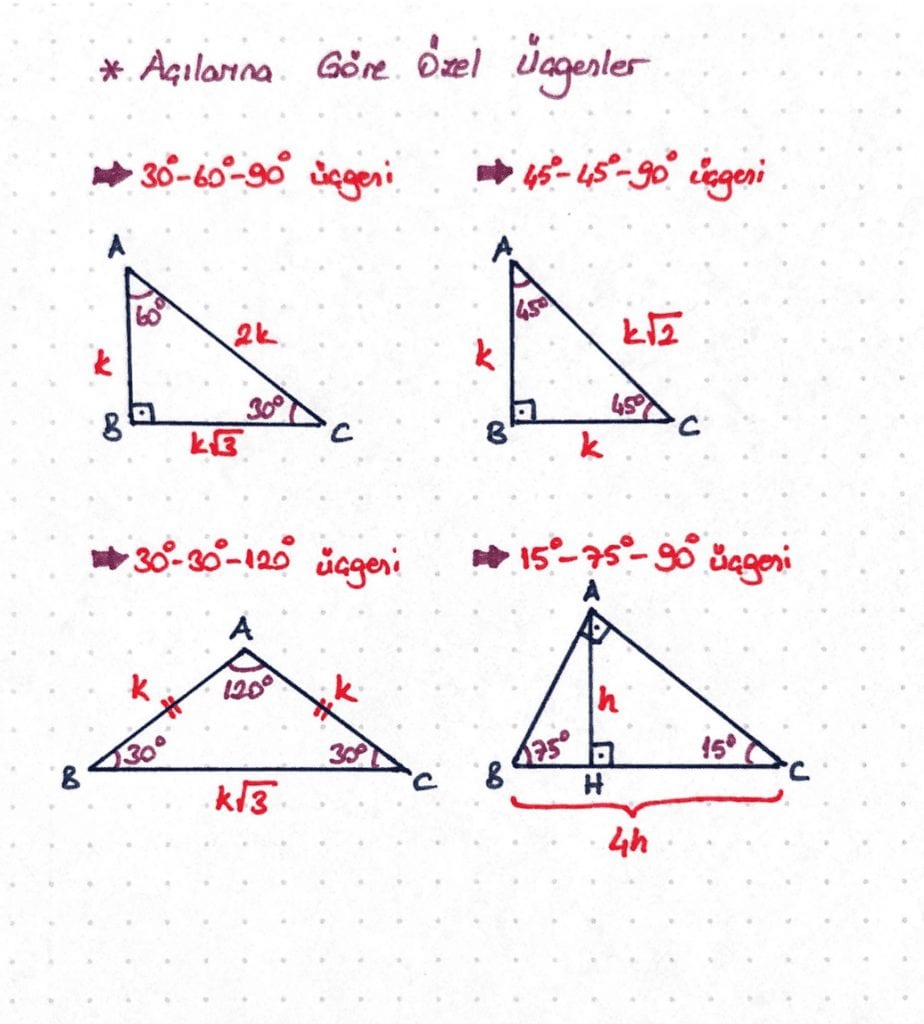
« 30 30 1 ÜÇgenİ 15 75 90 ÜÇGENİ → 9Sınıf Özel Üçgenler Konu Özeti ve Çözümlü Soruları sunusunun 45 45 90 ÜÇGENİ slaytını görüntülemektesinizüçgeni Bu üçgende 15°'lik açının karşısındaki kenar 1 cm ise 75°'lik kenarın karşısındaki kenar 2 3 {\displaystyle 2 {\sqrt {3}}} cm olur İspatı ise 22,567,590 üçgenindeki gibidir Tek farkı, 75°'lik açının 15° ve 60°'lik açılara bölünmesidir Ayrıca bu (15° 75° 90°) Üçgeni (15° 75° 90°) üçgeninde hipotenüse ait yükseklik AH = h dersek, hipotenüs BC = 4h olur Hipotenüs kendisine ait yüksekliğin dört katıdır




Dik Acili Ucgenlerin Ozellikleri Nelerdir Dik Ucgenlerin Temel Ozellikleri




15 75 90 Ucgeni Kurali Nedir 15 75 90 Ucgeni Ozellikleri Ve Sorulari
özel üçgenler (30°60°90° üçgeni) özel üçgenler (15°75°90° üçgeni) öklit teorimi Üçgeni Kenar Bağıntısı ( İSPAT ) tenten1 bu konuyu Geometri Formülleri forumunda açtı Cevap 2 Son mesaj 02 Ağu 13, 1933 üçgeni mrdanqerous bu konuyu Özel geometri soruları forumunda açtı Cevap 2 Son mesaj 18 Kas 12, 1806 ABC üçgeniDİK ÜÇGEN 16 15 75 90 ÜÇGENİ kaydeden Mustafa YAZAGAN 62 Kişisel Gelişim Geometri Psikoloji Science Harfler Eğitim Banyo Daha fazla bilgi Bunun gibi daha fazlası




3 4 5 Ucgeni Ve Ozellikleri Not Bu
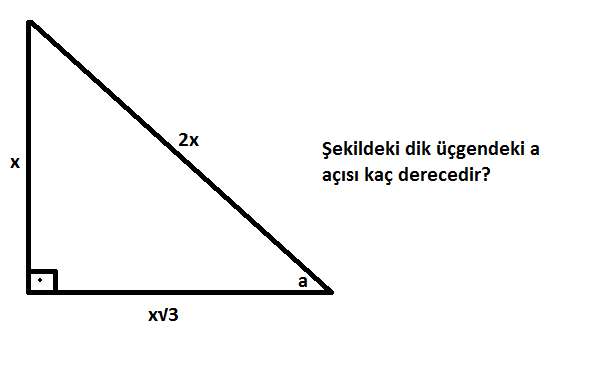



Acill Ozel Geometri Sorusu
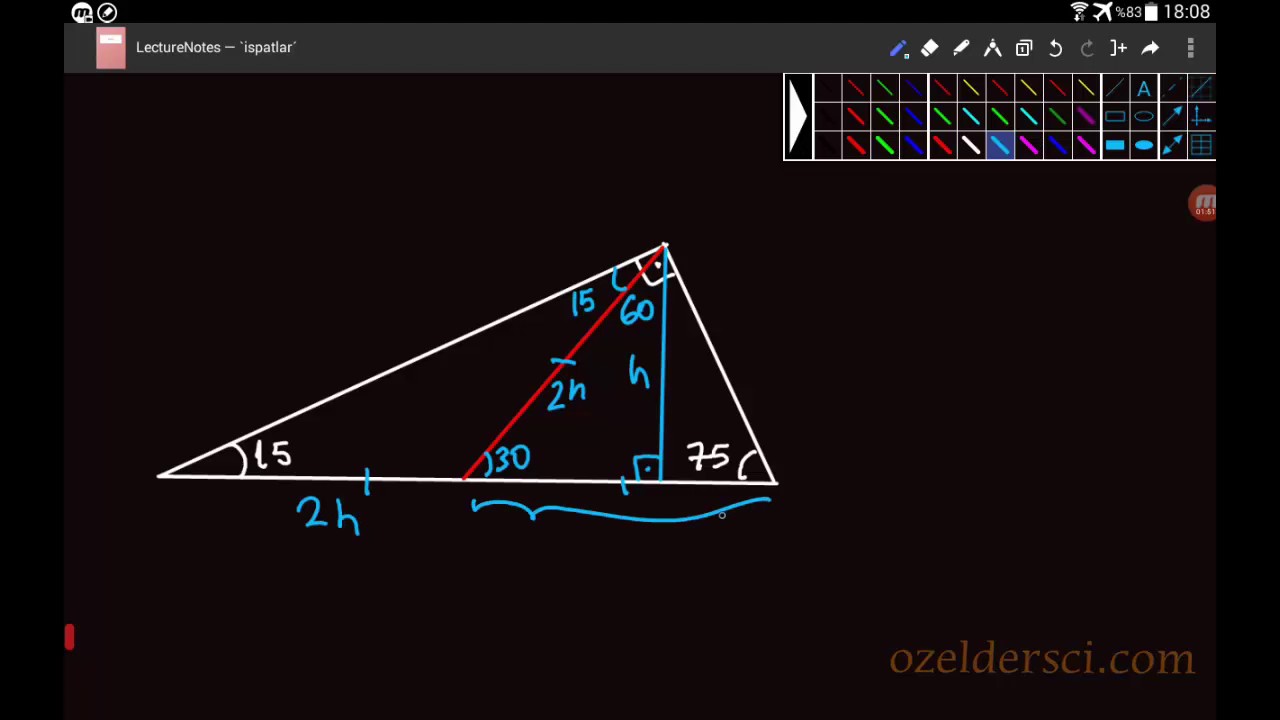
75 dereceyi 1560 derece olacak şekilde ayıran bir kenar çizip karşı dik kenar ile birleştirirsek, bir tarafta ikizkenar üçgen diğer tarafta üçgeni oluşur ve kenar uzunlukları arasındaki bağıntı ezberlenmemiş olur dik kenarlar arasındaki bağıntıyı hatırlayacak olursak, 15 in karşısındaki kenar "a" ise 75 in15 75 90 üçgeni 30 60 90 üçgeni 37 53 90 üçgeni 45 45 90 üçgeni 1 1 atalante #7593 2108 ~ 370 22,5 67,5 90 üçgeni oldum olası kim bulmuş diye merak ettiğim üçgendir lakin çözümü oldukça basittir 67,5 olan açıyı 22,545 olarak ayırırsınız, 15 75 90 üçgeni özelliklerinin ispatını gösteriyoruz, videomuzu izleyerek öğrenebilirsiniz SIFIRDAN MATEMATİK ÖĞRENİN İspat videolarımız ve dolayısı ile işin manasını, aslını, neyin nerden geldiğini anlatan ve bilginin kalıcı olmasını sağlayan videolarımız devam ediyor



1




Nedir Dik Acili Ucgenin Kenar Ve Aci Ozellikleri
See 75 photos and 12 tips from 149 visitors to cafe'riale "Enfes bitki caylari" Café in Ataşehir, İstanbul Hiçbir özelliği yok, Nestle Sicak Cikolata sadece 90 kalori s karaca Tatlılarının kremaları bayat, metalik ( ) ortadan bir dik çek , üçgeni olur 50 derecelik açının karşısındaki kenar 90cm olur x de hipotenüs olur sin50 = 90/x olur ,(15° – 75° – 90°) Üçgeni Geometri Konular 1°) Üçgeni, (30° – 60° – 90°) Üçgeni, (5 12 13) Üçgeni, İkizkenar dik üçgen, İKİZKENAR ÜÇGENI, ÖKLİT BAĞINTILAR, Üçgenlerde Uzunluk DİK ÜÇGEN Bir açısının ölçüsü 90° olan üçgene dik üçgen denir Dik üçgende 90




135 30 15 Ucgenini Aciklayabilir Misiniz Eodev Com




エレガント75 15 Ucgeni 最高のぬりえ
75 i 1560 diye böleceksin O 1515 ikizkenar oluşturacak diğer yerdede oluşacak uzunlukları taşıyacaksın tek tek Karede 15 varsa köşegen çekeceksin köşegenler açıortay olduğu için ve dik kesiştiği için oluşacak Cok basit aslinda bi numarası yok 15 75 90 üçgeni 2 ayrı çözüm yöntemi bulunur bunlardan bir tanesi 75 derecelik açıyı 30 ve 45 olarak, diğeri de 15 ve 60 olarak bölmektir 30 ve 45 olar(15 75 90) Üçgeni (45 45 90) Üçgeni (45 45 90) Üçgeni (45 45 90) Üçgeni konusunu önce anlatıyoruz hemen ardından etkileşime geçmesini sağlıyoruz Bu şekilde kalıcılığı ve öğrenmeyi sağlıyoruz Sizi ve arkadaşlarınızı sitemize bekliyoruz )
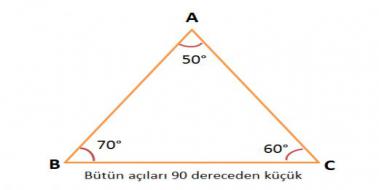



15 75 90 Ucgeni Ozellikleri Acilar Gen Tr
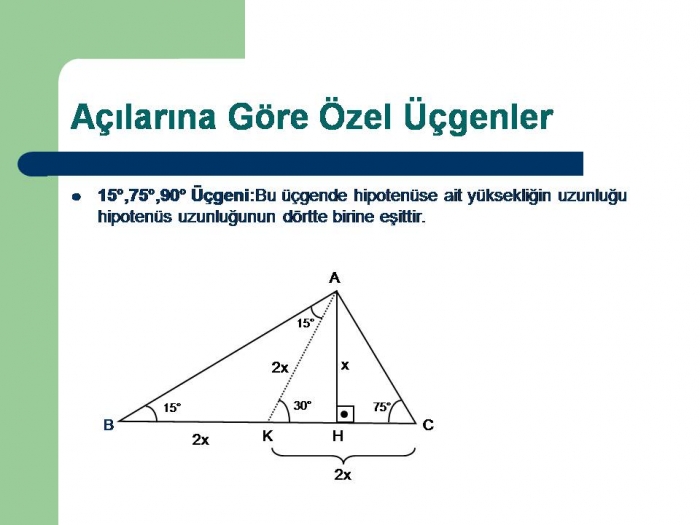



15 75 90 Ucgeni Uludag Sozluk
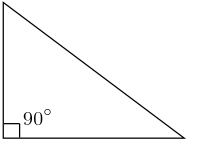
Bir açısının ölçüsü 90° olan üçgene dik üçgen denir Dik üçgende 90° nin karşısındaki kenara hipotenüs, diğer kenarlara dik kenar adı verilir Hipotenüs üçgenin daima en uzun kenarıdır şekilde, m (A) = 90° BC kenarı hipotenüs 30 60 90 Üçgeni 15 75 90 Üçgeni Özelliği Bu makaledeki notlar 15 75 90 üçgeninin özelliği 30 Özel Üçgenler DİK ÜÇGEN Bir açısının ölçüsü 90° olan üçgene dik üçgen denir Dik üçgende 90° nin karşısındaki kenara hipotenüs, diğer kenarlara dik kenar adı verilir 15 75 90 ÜÇgenİ kurali nedİr?




Rox Wood Aluminyum Ucgen Marangoz Gonye 175 Mm Fiyati



Www Nanomatematik Com Wp Content Uploads 21 03 7 Sinif 5 Unite Birlestirilmis Matematik Pdf
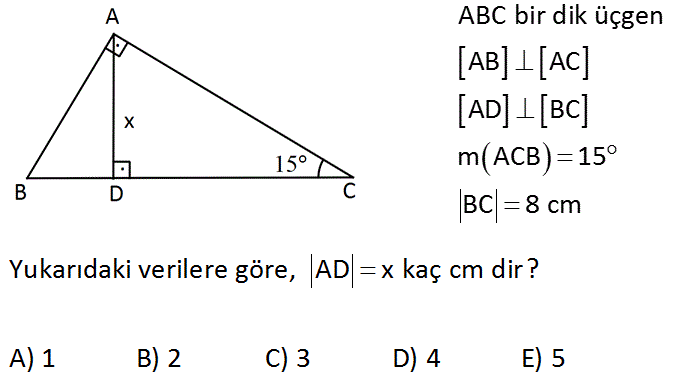
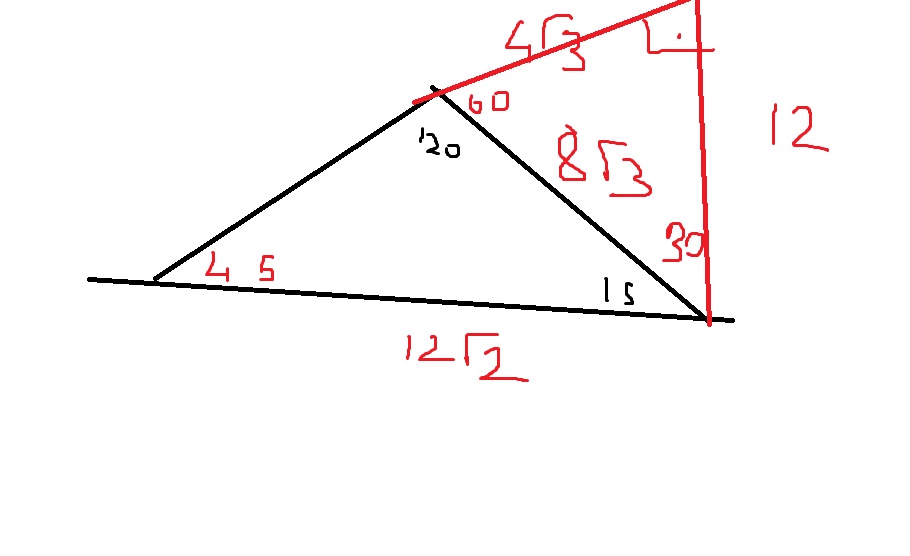
A) 2 2 B) 2 3 C) 3 2 D) 4 2 E) 6 Çözüm wwwmatematikkolaynet Üçgeni dışardan 45 45 90 üçgeni olacak şekilde uzatalımAB 6 6 12 birim buluruz 36 wwwmatematikkolaynet ABC üçgen, m ABC 30 m ACB 15 BC 6 2 cm Buna göre, AC x kaç cm dir? 15° 75° 90° üçgeni, Özel bir üçgendir Matematikte özel kavramı;
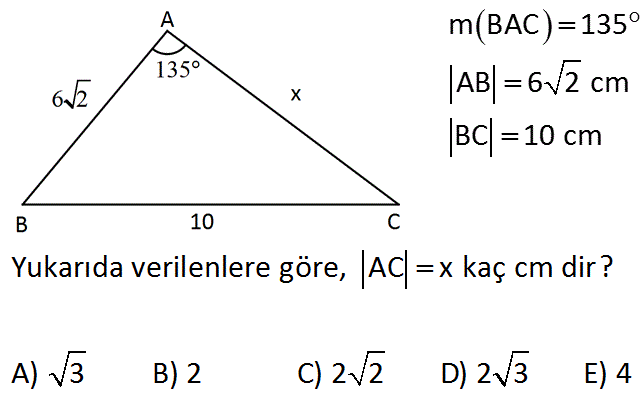



Ozel Ucgenler Formulleri



1
EBD üçgeni de ikizkenar bir üçgen olduğundan;Teoremin kendine has özelliklerinin olmasıdır Bu özellikler başka hiç bir teoremde yada cisimde bulunmamasıdır En önemlisi de teoremi çözebilmek için bazı kuralların ve formüllerin kullanmas–152 Tanaka Merotto et al (10) 75 SRAP markörünün C difformis için Danquah et al (02) 6 AFLP primeri ve 5 mikrosatellit primerinin E crusgalli' de polimorfizmi



Ozel Ucgenler Konu Anlatimi




15 75 90 Ucgeni Kurali Nedir 15 75 90 Ozel Ucgeni Ozellikleri Ve Ornek Sorular Egitim Haberleri
15 75 90 Üçgeni Geometri dersi için önemli özel üçgenlerden olan 15 75 90 üçgeni üçgenin sabit oranından gelmektedir Dik üçgen olan bu üçgende, diğer üçgenlerde olduğu gibi 15 75 90 üçgenin de kenarları arasında sabit oran bulunmaktadır Bu Üçgeni (h4h) İSPAT üçgeninde hipotenüse indirilen yüksekliğe h diyelim Daha Sonra Süper üçlüyü kullanmak için hipotenüsü iki eşit parçaya bölecek kenarortayı çizelim 3 adet üçgenimiz oluştu () () (0) 30⁰'nin karşısına h dediğimiz zaman 90⁰'nin karşısına 2h Dik açılı üçgenin özellikleri nedir?




15 75 90 Ucgeni




Dik Ucgen 17 22 5 67 5 90 Ucgeni Ders Calisma Ipuclari Evde Egitim Matematik
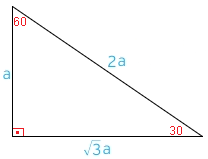
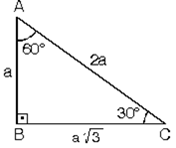
15 75 90 üçgeni özellikleri çoğu zaman dik bir üçgene dikme indirildiğinde ortaya çıkar Görselden de gördüğünüz gibi dik üçgenin, dik açısından tabana doğru bir dikme indirilmiş 15 75 90 üçgeni, üçgenler geometrinin temelini oluşturmaktadır Düzlemde doğrusal olmayan 3 noktanın birleşmesi ile oluşan geometrik şekildir Üç kenarı ve üç köşesi bulunan üçgenlerin 4 çeşidi bulunmaktadır Çeşitkenar üçgen, ikizkenar üçgen ve eşkenar üçgend 30 60 90 üçgeni dik üçgen sınıfında bir özel üçgendir Burada 30 derecenin karşısı 1 birim, 60 derecenin karşısı √3 birim, 90 derecenin karşısı olan en uzun kenar ya da hipotenüs ise 2 birim olur Yukarıda örnek bir 30 60 90 üçgeni verilmiştir Bu üçgene iyi bakmalıyız ki özellikleri aklımızda tutalım 30 60




15 75 90 Dik Ucgeni



En Hizli 30 60 90 Ucgeni Trigonometrik Oranlari Sorulari



Dik Ucgende Trigonometrik Hesaplamalar




Geometri Formulleri Sezgin Oner Matematik Yayinlari Facebook




Dik Ucgen Oklid Bagintisi 30 60 90 Ucgeni Kurali




Ozel Ucgenler Listesi



15 75 90 Ucgeninin Ozellikleri Nelerdir Ucgen Gen Tr




15 75 90 Ucgeni Not Bu




Ucgenin Alani Nasil Bulunur Ucgen Alan Formulleri Ve Cesitleri Bilgeniz Com



Dik Ucgen Vikipedi




Dik Ucgenler Pisagor Teoremi Konu Anlatimi Soru Cozumleri Ders Notu 9 Sinif Matematik Tyt



Dik Ucgen Vikipedi
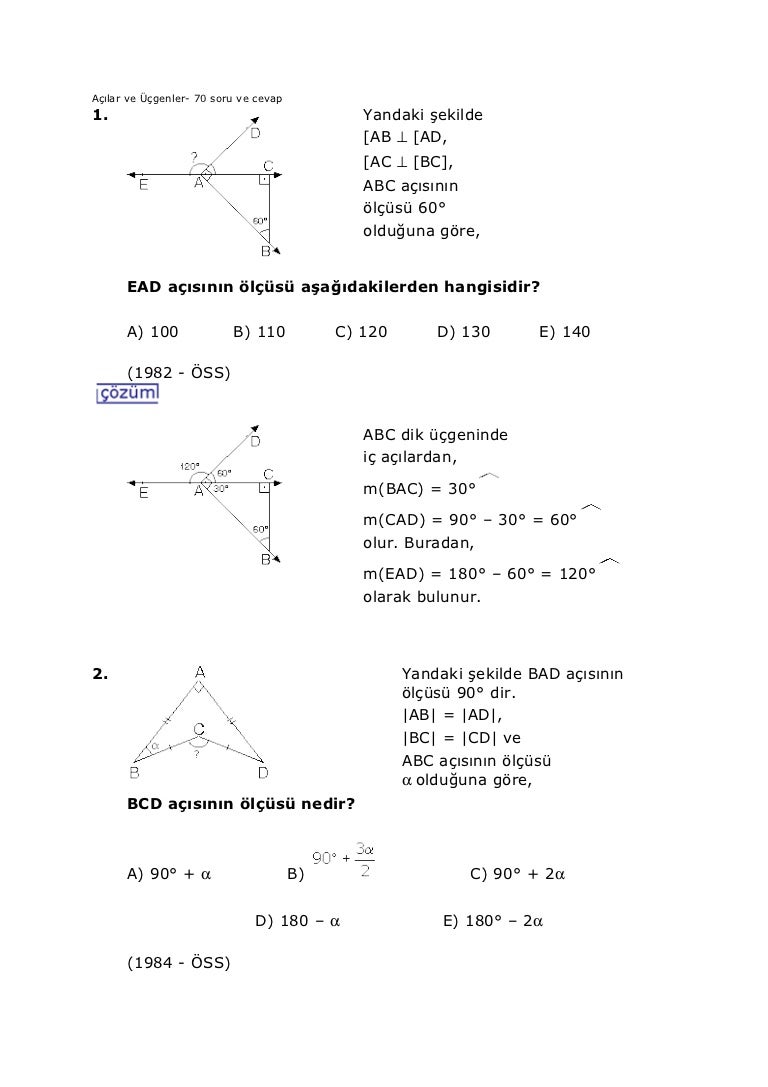



Acilar Ve Ucgenler




Ucgende Acilar Cozumlu Sorulari Ve Problemleri Matematik Ogretmenleri




15 75 90 Ucgeni Ucgende Acilar Ders Notlari Kunduz




15 75 90 Ucgeni Ozellikleri Ve Kurali Ogrenci Yardim




Matematik Formulleri Ozel Ucgenler 15 75 90 Ucgeni Wattpad
.JPG)



Ozel Ucgenler Acilarina Gore




Net Fikir Dik Ucgen Ve Temel Ozellikleri




Ozel Ucgenler Nelerdir Ozel Ucgenler 8 15 17 7 24 25 30 60 90 Ve Diger




Ozel Ucgenler Ders Notu Konu Anlatimi Ders Notu




15 75 90 Ucgeni Ozellikleri Ve Kurali Soru List



15 75 90 Ucgeni
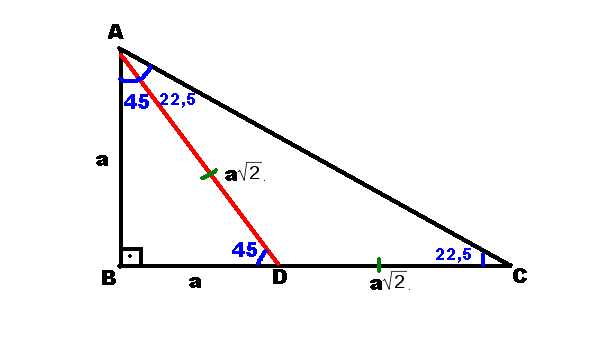



22 5 67 5 90 Ucgeni 1 2 Ispat




15 75 90 Ucgeni Ozellikleri Ve Kurallari
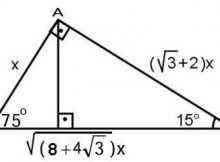



Ozel Ucgenler Not Bu




Ispat 15 75 90 Ucgeni Tyt Geometri Ozel Ucgenler Youtube
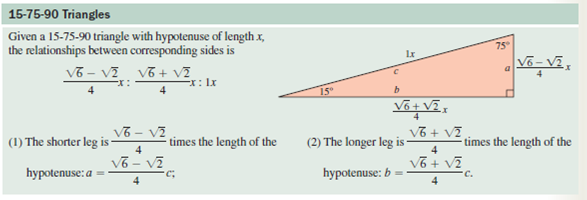



印刷可能 75 15 Ucgeni シモネタ




Geochemistry Of The Middle Jurassic Sediments In Gumushane North Eastern Turkey Implications For Weathering And Provenance Saydam Eker Geological Journal Wiley Online Library




Ucgende Acilar
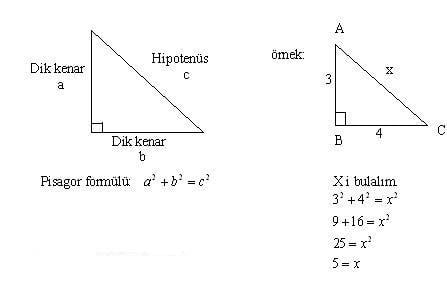



Dik Acili Ucgenin Kenar Ve Aci Ozellikleri Nedir



1
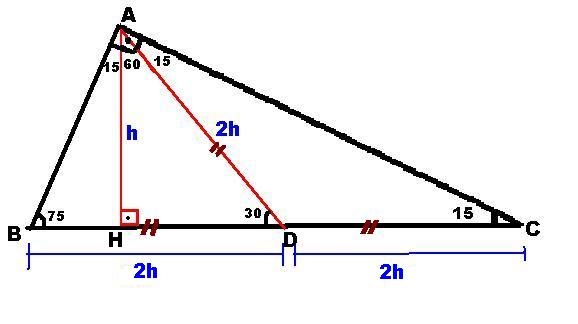



15 75 90 Ucgeni H 4h Ispat




Ucgen Ve Ozellikleri Pisagor Arican Fen Bilimleri Facebook




15 75 90 Ucgeni Akilli Geometri




Dik Ucgen Konu Anlatimi Ve Ornek Soru Cozumu Kunduz
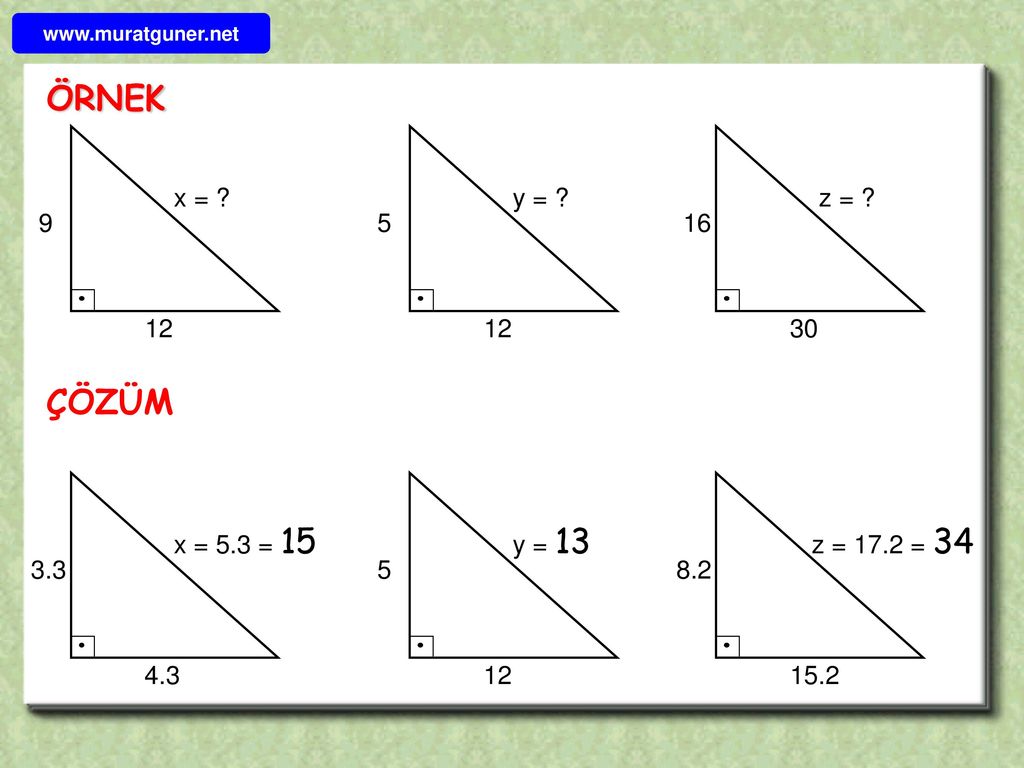



Matematik Ogrenebilir Ppt Indir




Dik Ucgen Konu Anlatimi Ve Ornek Soru Cozumu Kunduz
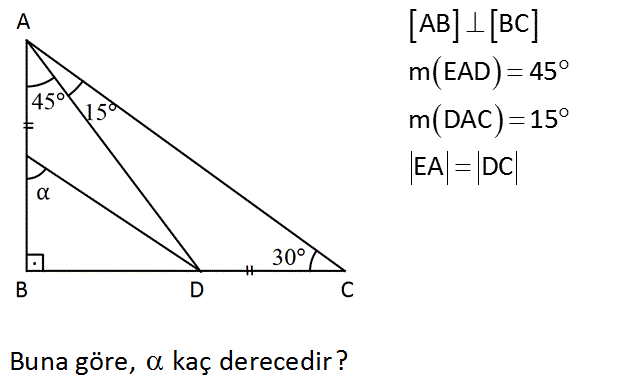



15 75 90 Ucgeni Ispati




15 75 90 Ucgeni Webders Net
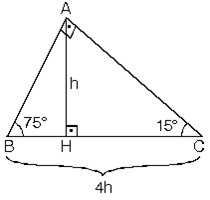



Dik Ve Ozel Ucgenler 1



9 Sinif Geometri Konu Ozeti Pdf Ucretsiz Indirin



Trigonometri Dik Ucgenlerdeki Trigonometrik Oranlar Matematikciler Com




Dik Ucgen Wikiwand




15 75 90 Ozel Ucgeninin Kenar Bagintilari Nedir Eodev Com




15 75 90 Ozel Ucgeni Oluyor Ama Ben Sadece O Ucgenin Yukseklik Le Ilgili Ozelligini Biliyorum Baska Eodev Com



Dik Ve Ozel Ucgenler 1



Dik Ucgen Konu Anlatimi Bilgicik Com Bilgicik Com




30 60 90 Ucgeni Ve Ozellikleri Not Bu



Dik Ucgende Trigonometri Bikifi



90 75 15 Ucgeni 90 75 15 Ucgeni Ozellikleri Ucgen Gen Tr




Dik Ucgen Oklid Bagintisi 30 60 90 Ucgeni Kurali




2 Kok 5 3 Ucgeni




Irklfzdethrwem



1




Dortgen Vikipedi Cute766




Dik Ucgen 6 15 75 90 Ucgeni Geometri Metin Hocam Youtube




15 75 90 Ucgeni Ucgende Acilar Ders Notlari Kunduz




Dik Ucgen 16 15 75 90 Ucgeni Temel Matematik Evde Egitim Matematik Felsefesi



Ozel Ucgenler Ozel Ucgenler Icindekiler Pisagor Bagintisi Oklit Bagintilari Kenarlarina Gore Ucgenler Acilarina Gore Ucgenler Kazanimlar Kaynakca Ppt Video Online Indir




Dik Ucgen Oklid Bagintisi 30 60 90 Ucgeni Kurali



15 75 90 Ucgeni Ucgende Acilar Ders Notlari Kunduz



Ozel Ucgenler Konu Anlatimi



Ozel Ucgenler Ppt Video Online Indir



45 45 90 Ucgeni Matematikce




Dik Ucgen Formulleri



Ozellik 5 Bilgicik Com Bilgicik Com



最新 75 15 90 Ucgeni シモネタ




Matematik Panosundaki Pin



15 75 90 Ucgeni



45 45 90 Ucgeni Matematikce




15 75 90 Ucgeninin Ispati




15 75 90 Ucgen Ozelligi Ve 5 Ornek Cozum Youtube
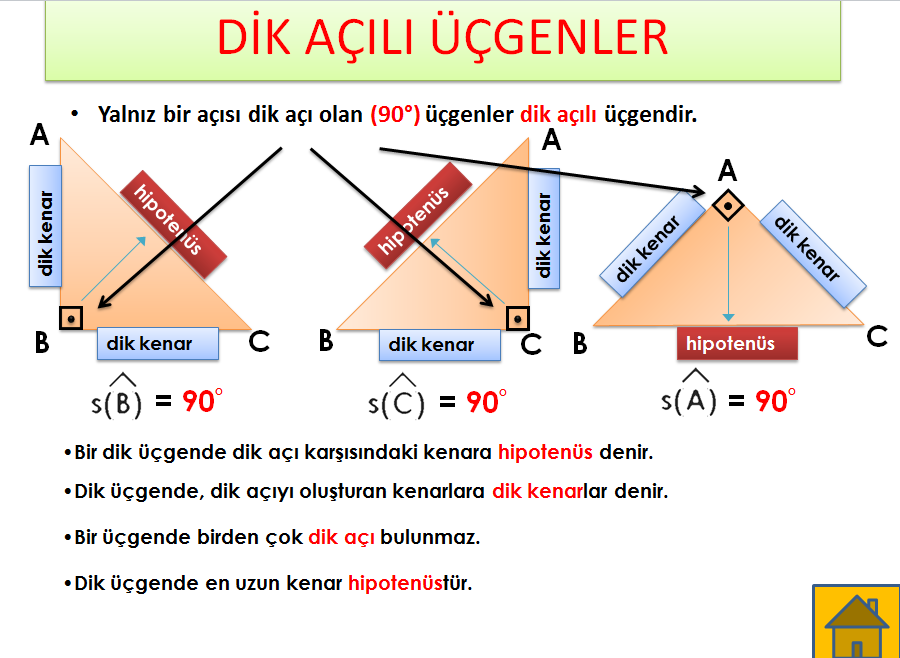



Dik Acili Ucgenin Kenar Ve Aci Ozellikleri Nedir
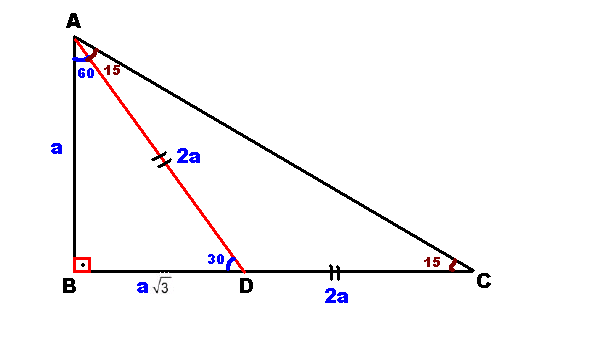



15 75 90 Ucgeni 2 3 Ispat




15 75 90 Ucgeni Ozelliklerinin Ispati Ozeldersci



0 件のコメント:
コメントを投稿